Гринвичское время и открытие долготы
- 1. Познание долготы: 300 г. до н. э. - 1675 г. н. э.
- 2. Гринвичское время для астрономов: 1675-1720 гг.
- 3. Гринвичское время для навигаторов: 1700-1840 гг.
- 4. Гринвичское время для Великобритании: 1825-1880 гг.
- 5. Нулевой меридиан 1790-1884 гг.
- 6. Гринвичское время для всего мира: 1884-1939 гг.
- 7. Часы, более точные, чем Земля
- Заключение
1. Познание долготы: 300 г. до н. э. - 1675 г. н. э.
Долгота в древние века
Понятия географических широты и долготы, определяющих местоположение какого-либо пункта на поверхности Земли, вероятно, возникли в древней Греции за 300 лет до нашей эры, но не в том виде, как мы понимаем их сейчас: сегодня широта - это количество градусов к северу или к югу от экватора, а долгота - количество градусов к востоку или к западу от некоторого выбранного меридиана. В эллинские времена эти величины наиболее часто, хотя и не всегда, выражали в интервалах времени: так, широту определенного пункта определяли родолжительностью самого длинного светового дня в году, разность долгот между двумя пунктами-различием их .^местных времен. Насколько нам известно, первым, кто предложил математически точную концепцию географической широты и долготы, был Клавдий Птолемей (ок. 90-160 гг. н.э.), который вместо традиционных временных координат привел в своей «Географии» сетку координат, исчисляемых в градусах, где широты измерялись от экватора, а долготы - от самой западной точки известного мира - «островов Фортуны» ( Канарские острова. - Прим) [1]. Большую часть своей жизни Птолемей провел за работой в знаменитой библиотеке г. Александрии, где и были созданы два его великих труда, под влиянием которых наука находилась вплоть до XVII в. Первый из них - это «Большое собрание» (Megale Sintaxis), более известное как «Альмагест» - книга, вобравшая в себя все наиболее ценное из древнегреческой астрономии; в ней Птолемей продолжил работы Гиппарха и Аполлония и в то же время привел много собственных результатов. Второй работой Птолемея была «География» - справочник и атлас известного в те времена мира, состоящий из восьми томов, где указывались географические положения многих тысяч пунктов. В обширном вводном руководстве по составлению карт, описывая определение географического местоположения, Птолемей обсуждает, в частности, методы определения долготы, предложенные тремя столетиями ранее Гиппархом из Никеи в Вифании ( Вифания находилась на северо-западе Малой Азии. - Прим. перев) (ок. 190-125 гг. до н.э.).
Уже во времена Гиппарха стало ясно, что определение разности долгот двух пунктов возможно по наблюдению (т.е. измерению местного времени) момента некоторого события в каждом из этих пунктов. В качестве такого события Гиппарх предложил использовать затмения Луны, так как ее вхождение в тень Земли и есть то событие, которое происходит в один и тот же момент для всех наблюдателей, где бы они ни находились на земной поверхности. Но, к сожалению, Гиппарх не указал способов, как измерить местное время в каждом из пунктов наблюдения. Непосредственно использовать для этой цели солнечные часы было невозможно, так как во время лунного затмения Солнце находится ниже горизонта. (Различные возможности этого способа определения долготы обсуждаются в приложении I.) При определении долготы методом лунного затмения возникали и другие трудности. Затмения случаются довольно редко: два-три раза в год, а иногда и совсем не происходят, поэтому определение долгот для большого числа пунктов требует длительного времени. В наследство потомкам Гиппарх составил таблицу затмений на шесть столетий вперед.
Другая трудность при наблюдениях лунного затмения заключается в том, что определить точный момент затмения нелегко. «Начало», «середина» и «конец» затмения для разных наблюдателей могут казаться разными, поэтому вполне вероятны ошибки по времени, в несколько минут, что соответствует нескольким градусам долготы. Несмотря на это, предложенный Гиппархом метод лунных затмений в течение последующих 1600 лет оставался единственным практическим методом, используемым для астрономического определения долгот.
В четвертой главе книги 1 «Географии», озаглавленной «Тщательно наблюдаемые явления должны быть более предпочтительны, чем те, которые выводятся из сообщений путешественников» (это один из тезисов Гиппарха, сформулированных тремя столетиями ранее), Птолемей описывает гиппарховский способ определения долготы по лунному затмению:
... и когда вслед за ним появились другие... вычисляющие большинство расстояний, особенно тех, что простирались к западу или востоку, исходя из некой общей традиции, и не из-за отсутствия мастерства или... вследствие лени части наблюдателей, а потому что в их время еще не существовало точной математики; к тому же наблюдалось немного затмений Луны в одно и то же время в разных местах; когда случилось затмение, в Арбеле было отмечено, что там оно произошло в пятом часу, из этого наблюдения было установлено, на сколько равноденственных часов [равных в противоположность неравным часам], или на какой промежуток времени, два пункта удалены один от другого на восток или запад; из этого ясно, что географ при написании географии должен положить в основу своей работы известные ему явления, изученные путем самого тщательного наблюдения... [2].
Затмение, на которое ссылается Птолемей, произошло непосредственно перед Арбельской битвой в 330 г. до н. э. и было зафиксировано в Арбеле и Карфагене с предполагаемой разностью местных времен в три часа. (Действительная разница должна была составить 2 ч 15 мин.) Это, кажется, было единственным астрономическим определением разности долгот, которое Птолемей использовал в своей «Географии» [3].
Прошло более тысячелетия, прежде чем удалось сколько-нибудь существенно усовершенствовать метод определения долготы. Два крупнейших события в истории определения долготы в море относятся к последним десятилетиям XIII в. Во-первых, в Европе были изобретены первые механические часы-одно из самых важных изобретений средневековья. Само название часы ( The clock (англ.). - Прим. перев) - по латыни clocca означает колокол - говорит о том, что самые первые часы поначалу отсчитывали (отбивали) время для религиозных и мирских нужд, и только позднее они стали астрономическими и навигационными инструментами.
Во-вторых, появилась морская карта, самая древняя ссылка на которую найдена в описании времен Людовика IX (Святого) и восьмого крестового похода в 1270 г. Большинство ученых считают, что в те времена должен был существовать какой-то вид морской карты. Морская карта, насколько известно, получила распространение в Италии; обычно вычерченная чернилами на целой коже тонкого пергамента, она давала изображение Средиземного моря. Такая карта сопутствовала portolano, или штурманской книге (поэтому такие карты перешли в XIX в. под названием «портулановских карт») [4]. Древнейшая из дошедших до наших дней карт-это карта Средиземноморья, не имеющая ни подписи, ни даты, на которой отсутствует сетка широт и долгот [5]. Очевидно, она была нарисована где-то около 1300 г.
Век открытий
В начале XV в. торговля между Европой и Азией велась либо через Черное и Средиземное моря, либо по суше и почти полностью была сосредоточена в руках итальянских морских государств - Венеции и Генуи. Отрезанная от этих рынков Португалия устремилась к югу, решив распространить свое влияние на море. Уже в XIV в. она стала привлекать к себе на службу для создания морского флота генуэзских штурманов. Один из сыновей короля Ионна I принц Энрико (названный впоследствии Энрико Мореплавателем), губернатор южной провинции Алгарви, из своей резиденции Сагриш вблизи мыса Сан-Висенти нанимал на службу арабских математиков - они должны были инструктировать его капитанов по искусству навигации в Атлантическом океане, которое требовало совершенно иных навыков, чем мореплавание в Средиземном море.
Со временем на пожертвования ордена Христа, главным магистром которого являлся принц Энрико, Португалия снарядила корабли, которые, плавая на юг и вокруг Африки, открыли морской путь на Восток. В 1434 г. португальские мореплаватели достигли мыса Бохадор, самой южной точки Канарских островов, в 1444 г. - мыса Зеленого, в 1487 г. - мыса Доброй Надежды; усилия Португалии на море достигли своей наивысшей точки в 1498 г., когда Васко да Гама достиг г. Каликут на Малабарском побережье Индии.

1. Альманах Региомонтана, 1474. На этой странице показаны предвычисленные полные затмения Луны для 1504 г., с помощью которых Колумб поразил воображение туземцев Ямайки. (Королевское астрономическое общество.)
Эти океанские путешествия, эти плавания в неизведанное способствовали развитию новых идей в навигации и обусловили использование астрономических методов определения местоположения в дополнение к уже испытанным временем способам измерения при помощи компаса, лотлиня и по оценке скорости корабля. Португалия достигла значительных успехов в изобретении методов и инструментов, позволяющих определять широту по наблюдениям Полярной звезды и Солнца. Протяженность океанского маршрута в северо-южном направлении не имела значения для определения местоположения корабля, но плавание вокруг мыса Доброй Надежды, т. е. движение в западно-восточном направлении, было очень важно, в особенности для Христофора Колумба, отплывшего с Канарских островов в сентябре 1492 г.
Некоторые исследователи пытались определять долготу из астрономических наблюдений. С этой целью Колумб захватил с собой в плавание библиотечку, включающую альманахи и эфемериды, составленные Иоганном Мюллером (прозванным Региомонтаном, от лат. Regiomontanus - Кёнитсбергский). Мюллер предвычислил каждодневные положения Солнца, Луны и планет для Нюрнберга на период 1476-1506 гг. [6]. Позднее его эфемериды были продолжены Стоффлером из Тюбингена до 1531 г. [7]. Во время своего второго путешествия Колумб, пока его корабль стоял в испанской гавани, наблюдал затмение Луны 14 октября 1494 г. Полученная им долгота отличалась на 23° к западу от истинной, что в единицах времени соответствует 1,5 ч [8]. Во время четвертого плавания, когда 29 февраля 1504 г. корабль находился на Ямайке, Колумб, воспользовавшись предвычисленным моментом затмения Луны, сначала разыграл перед туземцами роль божественного провидца (подобное событие 350 лет спустя Марк Твен описал в своем произведении «Янки при дворе короля Артура»), а затем из наблюдений определил долготу своего местонахождения, но с ошибкой в 2,5 ч к западу. (Что было причиной этих ошибок - неточность в определении местного времени, ошибки альманаха Региомонтана, а может быть, просто желание Колумба доказать, что он действительно достиг берегов Азии, -этого мы никогда не узнаем [9].) 14 августа 1499 г. во время своего второго путешествия Америго Веспуччи наблюдал затмение Марса (покрытие этой планеты Луной) и определил долготу своего местонахождения - 1366 2/3 лье (82°) к западу от г. Кадис [10] - с такой точностью, к которой трудно придраться. Но методы, применявшиеся Колумбом и Веспуччи, нельзя было использовать часто, и, кроме того, они давали приемлемые результаты только на стоянке. Поэтому в последнем десятилетии XV в. возникла крайняя необходимость в решении проблемы определения долготы в открытом море, что в конечном счете привело к основанию Гринвичской обсерватории и установлению гринвичского времени
Определение долготы методом лунных расстояний
Правильное решение названной проблемы было уже не за горами. В 1514 г. Иоганн Вернер (1468-1522) из Нюрнберга опубликовал новый перевод 1-й книги птолемеевской «Географии» [11]. В своих комментариях к четвертой главе (несколько строк из которой мы уже цитировали) Вернер предложил впредь для определения долготы воспользоваться новым методом, названным им методом лунных расстояний, а для наблюдений применять поперечный жезл - инструмент, созданный на основе жезла Якоба, изобретенного за двести лет до этого прованским астрономом Леви бен Герзоном [12].
Тем не менее прошло еще почти 250 лет, прежде чем появилась практическая возможность измерять долготу в открытом море методом лунных расстояний. (Более подробно об этом говорится в приложении I.) В этом методе используется то, что Луна сравнительно быстро перемещается на фоне звезд зодиакальных созвездий, передвигаясь за час на расстояние, примерно равное ее диаметру. «Таким образом, географ прибывает в один из выбранных пунктов и в любой известный момент времени ведет оттуда при помощи этого инструмента [поперечного жезла] наблюдения расстояния между Луной и одной из опорных звезд, расположенных вблизи (или на самой) эклиптики» [13]. Так писал Вернер, предлагая, между прочим, использовать этот метод на суше. Затем с помощью астрономических таблиц положений звезд и альманаха с предвычисленными положениями Луны можно определить разность долгот между наблюдательным пунктом и тем местом, для которого был составлен альманах. Однако все это было хорошо только в теории. На практике же ни инструментов, ни точных таблиц, позволяющих получить удовлетворительные результаты, в то время не существовало. Более того, Вернер не принял во внимание лунный параллакс - явление, вследствие которого для наблюдателей, находящихся в разных пунктах на поверхности Земли, положение Луны на небесной сфере оказывается различным. Для получения точных результатов учет параллакса был совершенно необходим.
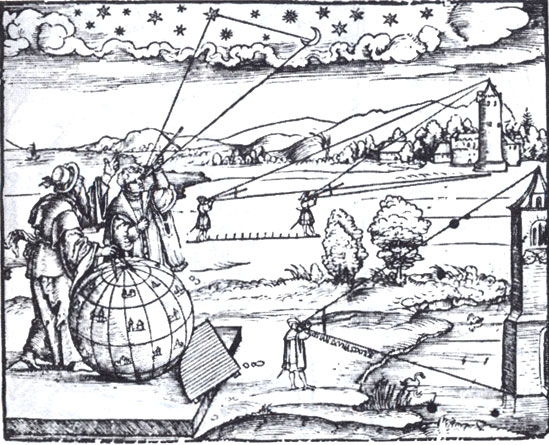
2. Наблюдения с помощью поперечного жезла, используемые для определения лунных расстояний и измерения высот зданий. Эта гравюра была приведена на титуле труда Петра Апиана 'Введение в географию' (Introductio Geographica Petri Apiani in Doctissimus Verneri Annotationes...), Ингольштадт, 1533. (Британская библиотека.)
Морякам и ученым метод лунных расстояний был известен не в том виде, как он описывался Вернером, - они знали его наглядное, как хорошая картина, описание, приведенное в «Космографии» (Ингольштадт, 1524) Петра Апиана (1495-1552) [14]. Этот труд в 1533 г. был переиздан Геммой Фризием (1508-1555), фризийским астрономом и математиком [15], и успешно публиковался до конца шестнадцатого столетия. В Англии первое описание метода лунных расстояний было сделано Уильямом Канингэмом из Нориджа в 1599 г. в книге «Космографическое зеркало», написанной прекрасным языком и отпечатанной великолепным итальянским шрифтом:
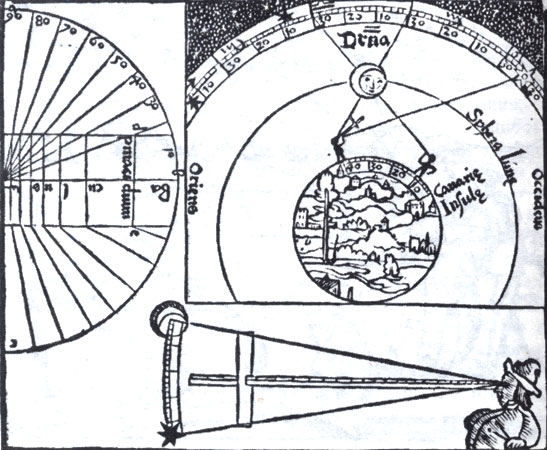
3. Древний рисунок, иллюстрирующий определение долготы методом лунных расстояний, из первого издания труда Петра Апиана 'Космография' (Инголыптадт и Ландшат, 1524). (Бодлеанская библиотека, Оксфорд.)
Я открою вам, какие три вещи необходимы для этого дела. Первое-это астрономический жезл, называемый также жезлом Якоба (подобный которому вы можете найти среди других инструментов), второе - истинное положение Луны в поясе Зодиака в градусах и минутах в тот момент, когда вы производите наблюдение (его можно взять из эфемерид), и третье - долгота опорной звезды, которую можно получить из таблицы опорных звезд, помещенной в моей первой книге. Имея все это, вы должны взять ваш стержень с прикрепленной к нему поперечной рейкой и навести один конец рейки на центр Луны, а другой - на подходящую звезду, затем передвигать рейку вверх и вниз до тех пор, пока концы стержня не соединят центры Луны и звезды. После этого рейка укажет вам расстояние Луны от звезды в градусах и минутах. Зная расстояние в градусах и минутах между Луной и опорной звездой, которое вы имели до наблюдения, и вычьтя эти расстояния одно из другого, вы получите разность. Если вы поделите эту разность на величину, на которую перемещается Луна за один час, то это даст вам момент, когда Луна находилась за звездой (если звезда расположена к западу от нее) или когда она будет перед звездой, если звезда была восточнее Луны [16].
Изобретение хронометрического метода
Первым, кто предложил воспользоваться часами для определения долготы в море, был упомянутый выше Гемма Фризий. В своей работе «Принципы астрономической космографии», вышедшей в Лувене в 1530 г., в главе 19, озаглавленной «Содержание нового метода определения долготы» он пишет:

4. Хронометрический метод определения долготы - английское описание, 1559 г. Из труда У. Канингэма 'Космографическое зеркало' (The Cosmographical Glasse, 1559). (Национальный морской музей.)
В нашем веке мы имеем некоторое количество небольших искусно изготовленных часов, находящих себе определенное применение. В связи с их небольшими размерами эти часы необременительны в путешествии. Часто они могут идти непрерывно свыше 24 ч. А с вашей помощью они смогут идти вечно. Используя такие часы и некоторые методы, можно определить долготу. Прежде чем отправиться в путешествие, мы должны позаботиться о том, чтобы точно найти время в исходном пункте, из которого мы отправляемся. Когда мы отойдем на 15-20 миль, пожалуй, можно узнать разность долгот между тем местом, которого мы достигли, и местом нашего отправления. Мы должны подождать до тех пор, пока часовая стрелка наших часов не подойдет точно к часовой отметке циферблата, и в этот же момент с помощью астролябии или глобуса определить время в том месте, где мы находимся. Если это время с точностью до минуты совпадает с тем временем, которое показывают наши часы, то можно быть уверенным, что мы до сих пор находимся на том же самом меридиане, или на той же долготе, и наше путешествие проходило в южном направлении. Но, если эта разность достигнет одного часа или некоторого количества минут, тогда эти величины мы должны перевести в градусы или градусные минуты методом, который я описывал в предыдущей главе, и таким образом получить долготу. При помощи этого способа я могу определить долготу любого места, даже если я неожиданно прошел тысячу миль и даже если расстояние, которое я прошел, мне неизвестно. Но прежде всего, как всегда, нужно определить широту. Я уже рассказывал, как это сделать, а также объяснил, каким образом ее можно получить при помощи методов, связанных с определением времени. Итак, действительно нужно иметь очень надежные часы, не меняющие свой ход при изменении окружающих условий [17].
В издании 1533 г. есть изречение, в котором, кажется, впервые упоминается об определении долготы в море:
Таким образом, в длительных путешествиях, особенно морских, полезно пользоваться большими клепсидрами (водяными часами) или песочными часами, которые смогут точно измерять время круглые сутки и благодаря которым можно исправлять ошибки других часов [18].
В 1555 г. Ричард Эден перевел это описание на английский язык и добавил к нему собственный постскриптум:
И таким путем долгота будет найдена. При помощи этого искусства я смогу найти долготу местоположения, даже если я буду находиться за тысячу миль от избранного мной курса и на неизвестном расстоянии, но для этого сначала должна быть хорошо известна широта. Конец [19].
Но все это пока оставалось лишь мечтой, которая осуществилась только через два столетия.
На эту же тему Канингэм написал трактат в форме диалога между «собеседниками» Филоникусом и Сподиусом, страница которого воспроизведена на рис. 4 [20].
Долготные призы
Хотя теоретически, казалось, все было ясно, настоятельно требовалось практическое решение вопроса об определении долготы, причем не только в море, но и на суше; к этому побуждало развитие океанских путешествий, а также все возрастающая зависимость ряда стран от торговли с Вест-Индией.
В 1567 г. испанский король Филипп II назначил вознаграждение за решение проблемы определения долготы в открытом море. В конце столетия Мигель Сервантес и другие испанские писатели острили по поводу попыток некоторых «сумасшедших» определить местоположение в море - el punto fijo [21]. «Определение долготы», как и «квадратуру круга», стали отождествлять с чем-то в сущности неразрешимым; так, математик из «Новеллы о беседе собак» Сервантеса говорит:
Вот уже двадцать два года, как я стараюсь отыскать неподвижную точку [punto fijo]: то она у меня пропадает, то снова находится; стоит мне только поверить, что я ее нашел и что она от меня больше не уйдет, смотришь - опять я от нее так далеко, что просто диву даешься! Не лучше обстоит у меня дело и с квадратурой круга: одно время я был так близко к цели, что до сих пор мне кажется, будто решение лежит у меня в кармане... [22].
В 1598 г. Филипп III обещал вознаграждение - 6 тыс. дукатов в качестве постоянного взноса, 2 тыс. дукатов в виде пожизненной ренты и 1 тыс. дукатов для оказания помощи-любому, кто сможет «открыть долготу». Полностью этого приза не удостоился никто, но для поощрения возможных изобретателей были выплачены значительные суммы. Гулд упоминает о семи случаях вознаграждений за период 1607-1626 гг., большинство из которых было связано с работами по созданию компасов и по магнетизму [23]. Приблизительно в то же время Соединенные провинции Голландии назначили приз в 30 тыс. флоринов [24]. Вознаграждение обещали также Португалия и Венеция [25].
Очевидно, самой известной личностью среди причастных к испанскому призу был итальянский астроном Галилео Галилей (1564-1642). С помощью недавно изобретенного телескопа он сделал одно из своих первых блестящих открытий, а именно обнаружил у Юпитера четыре спутника, которые при наблюдениях с Земли с периодами от 1,75 до 17 сут появлялись и исчезали, скрываясь за Юпитером или попадая в тень планеты. Затмения и покрытия всегда происходили фактически в один и тот же момент для любого наблюдателя, в какой бы точке земной поверхности он ни находился. Галилей понял, что это явление можно использовать как самые совершенные небесные часы, которыми, если затмения будут заранее предвычислены, можно воспользоваться для определения долготы подобно тому, как в свое время Гиппарх предлагал использовать затмения нашего спутника, Луны. Метод Галилея обладал дополнительным преимуществом вследствие того, что затмения юпите-рианских спутников происходят много чаще: один-два раза за ночь.
Но этот метод обладал и недостатками: во-первых, для того чтобы им воспользоваться, был необходим телескоп, который, как считалось, применять в море затруднительно (позднее это стало возможным); во-вторых, сами затмения происходят не мгновенно. Однако Галилей, уверенный в том, что эта задача разрешима, занялся изучением движения юпитерианских спутников и составил таблицы, предсказывающие моменты затмений. В 1616 г. в надежде выиграть «долготный приз», он предложил свой метод Испании. На испанцев этот метод впечатления не произвел, и в 1632 г. после продолжительной переписки Галилей, по всей видимости, оставил мысль о его продаже Испании. В 1636 г. Галилей попытался предложить свой проект Голландии, отмечая, что он потратил двадцать четыре года на совершенствование своих таблиц. В отличие от Испании Соединенные провинции Голландии заинтересовались предложением Галилея, но переговоры шли с трудом. В это время Галилей находился фактически под домашним арестом в Арсетри вблизи Флоренции, пребывая под тайным надзором инквизиции, которая не позволила ему даже принять золотую цепь, подаренную правительством Голландии. Смерть Галилея, последовавшая в 1642 г., положила конец всем переговорам.
Достижения семнадцатого столетия
Исследуя колебания маятника как механизма, позволяющего регулировать ход часов, Галилей внес новый вклад в развитие искусства измерения времени, а также в историю определения долготы. Первое упоминание об использовании гиревых часов в астрономии относится к 1484 г., когда Бернард Уолтер, ученик Региомонтана, применил такие часы для измерения промежутка времени между моментами восходов планеты Меркурий и Солнца [26]. Часы были неотъемлемой частью астрономического инструментария, которым пользовался знаменитый датский астроном Тихо Браге (1546 1601); составленный им каталог 777 звезд, расширенный до 1005 звезд и опубликованный современником Галилея Иоганном Кеплером (1571-1630) в его Рудольфовых таблицах в 1627 г. [27], оставался самым совершенным вплоть до основания в 1675 г. Королевской обсерватории. Тихо Браге приобрел и испытал в период 1577-1581 гг. четыре экземпляра часов, после чего пришел к заключению, что из-за дефектов часового механизма эти часы непригодны для решения большинства астрономических задач.
В 1637 г. Галилей первым обратил внимание на то, что длина маятника может служить элементом, регулирующим ход часов, однако ему так и не удалось практически усовершенствовать часовой механизм. Под действием силы тяжести маятник совершает естественное, регулярное движение. Это явление, называемое изохронностью, означает, что колебания маятника происходят с равными помежутками времени, почти не зависящими от угла отклонения маятника и веса его груза. Период колебания маятника, однако, связан с его длиной и поэтому легко регулируется.
Галилей произвел соответствующие расчеты для самых простых маятниковых часов со спусковым механизмом (см. приложение III), поддерживающим непрерывное движение маятника. Тем не менее, насколько нам известно, реальные часы по этим расчетам так никогда и не были изготовлены. Честь изобретения маятниковых часов - но не открытия изохронности маятника-принадлежит голландскому математику, астроному и часовых дел мастеру Христиану Гюйгенсу (1629-1695). Изобретение в 1657 г. маятниковых часов и балансной часовой пружины - в 1670-х гг., в разработке которой Гюйгенс также принимал участие, следует рассматривать как основные этапы в развитии науки измерения времени.
Прежде чем более подробно говорить о работах Гюйгенса и его хранителях времени, вспомним теоретические разработки тех лет, связанные с определением долготы. В 1634 г. Жан Батист Морин, доктор медицины и профессор математики Королевского колледжа в Париже, заявил, что он открыл секрет долготы. Для изучения этого открытия кардинал Ришелье учредил комиссию в составе адмирала и пяти ученых. Астролог, свято верящий в систему мира Птолемея, согласно которой Земля является центром Вселенной, Морин не доверял часам и поэтому писал, что не знает, достигнет ли дьявол успеха в изготовлении долготного хранителя времени, но пытаться это сделать человеку - просто безумие [28]. Сам же Морин предлагал применить для определения долготы описанный выше метод лунных расстояний, однако с учетом очень важного явления-лунного параллакса. С точки зрения геометрии метод Морина был верен, но, как решила комиссия, он не поможет определить долготу, так как таблицы положений звезд и Луны настолько несовершенны, что не позволят применить его на практике. Тогда Морин, рассчитывая на вознаграждение, обратился к Голландии, и тоже безуспешно. Все же в конце концов преемник Ришелье кардинал Мазарини в 1645 г. назначил Морину пенсию в размере 2 тыс. ливров.
После изобретения в 1657 г. маятниковых часов Гюйгенс обратился к проблеме измерения долготы, будучи уверен, что именно с помощью часов-морского хранителя времени, который сможет хранить время в течение многих месяцев в любых климатических условиях, несмотря на движение корабля, - вскоре представится возможность определить долготу. Поэтому в последующие годы он усердно занимался изготовлением разнообразных морских хранителей времени, которые в период 1662-1687 гг. испытывались в морских путешествиях. В 1668 г. один из хронометров Гюйгенса, выдержав два шторма и морское сражение, позволил определить разность долгот между Тулоном и Критом; полученный результат, 20° 30', отличался от истинного значения, 19° 13', всего на 100 км (если ошибку выразить в единицах длины) [29]. Ход первых хронометров Гюйгенса, регулируемых маятником (если хронометры подвергались качке), был очень беспорядочен. Поэтому в 1674 г. Гюйгенс отказался от маятника и предложил в качестве регулятора хода морского хронометра использовать баланс и балансную пружину. Это был смелый шаг, но, как мы увидим, должно было пройти еще сто лет, прежде чем появилась возможность изготовить по-настоящему удовлетворительный морской хронометр.
Морин, после того как его предложения по определению долготы были в 1630-х гг. отвергнуты, вдохновился идеей о создании обсерватории, которая позволила бы получать данные, необходимые для практических целей. При Людовике XIV, в 1667 г., в значительной степени благодаря стараниям министра финансов Франции Жана Батиста Кольбера, была создана Парижская обсерватория как часть основанной в предыдущем году Королевской Академии наук. Это предопределило ведущее место Франции в науке, а следовательно, обусловило ее господство и на море. Для сотрудничества с французскими учеными, такими, как Жан Пикар, Адриан Озу и Филипп де ла Гир, в Парижскую обсерваторию были приглашены с назначением им высоких окладов многие знаменитые иностранные ученые, среди которых были Христиан Гюйгенс из Лейдена, Оле Рёмер из Копенгагена и Джованни Доменико Кассини из Болоньи.
Британский эквивалент Французской Академии наук - Королевское общество Лондона для совершенствования естественнонаучных знаний было основано Карлом II четырьмя годами раньше, в 1662 г. «Определение долготы» было одним из многих предметов натурфилософии, которые привлекли к себе внимание только что созданного научного общества. Ниже цитируется 26-я строфа поэмы «В честь избранной компании философов и остряков, которые встречаются еженедельно по средам в Грешэмском колледже»:
26. Наш колледж вскоре целый мир измерит, Который невозможно и объять. И каждый навигатор пусть поверит, Что сможет долготу свою узнать. И без труда до антиподов Любой корабль доставлен будет моряком.
Эта поэма, по-видимому, была написана около 1661 г., за год до того, как король подписал хартию об основании Королевского общества. Поэма состоит из двадцати восьми строф, первые двадцать шесть из которых посвящены описанию разнообразных проектов, рассматриваемых зарождавшимся обществом: лунному глобусу Рена, воздушному насосу Бойля, экспериментам с намагниченными опилками, пожиранию одежды молью, водолазному колоколу Эвелина, гравированию и травлению [30].
Прежде чем перейти к истории гринвичского времени, заметим, что Французскую Академию в то время занимали два вопроса. Одним из планов, принятых академией, предусматривалось составление новых карт Франции на основе измерения долгот методом Галилея - из наблюдений спутников Юпитера.
Новая топографическая съемка, произведенная Кассини и Пикаром, подтвердила, что старые карты завышали истинные размеры Франции. Король, недовольный очевидным изменением подвластной ему территории, как утверждают, сказал, что его топографы урезали территорию его страны в гораздо большей степени, чем его армия ее увеличила.
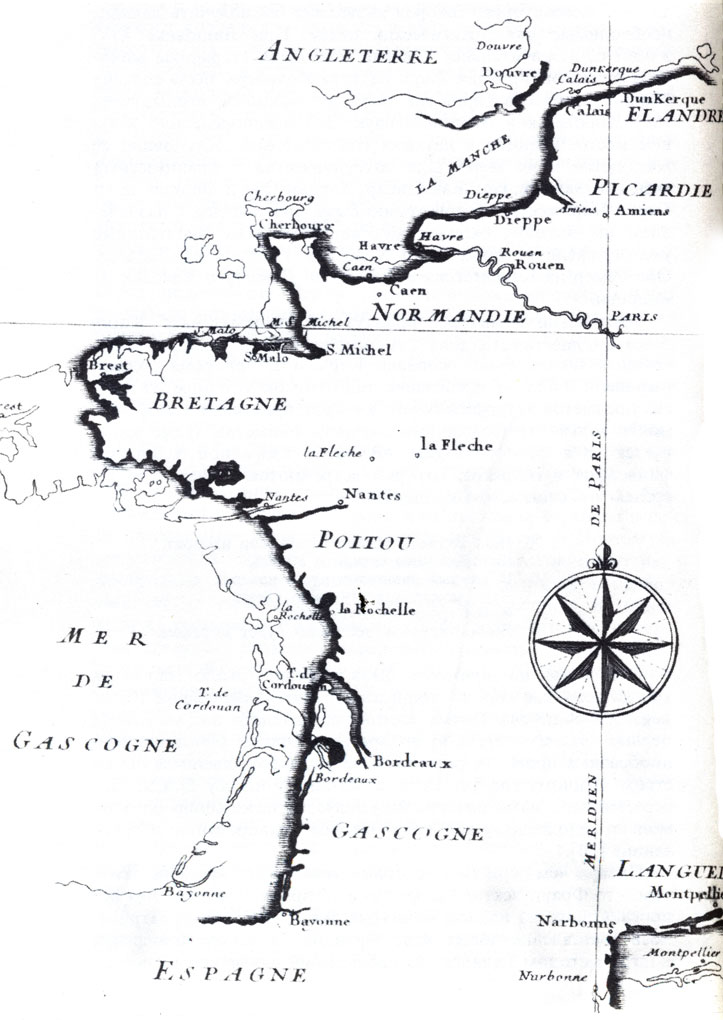
5. Повторная картографическая съемка территории Франции. Тонкой линией показана карта Франции до съемки. (Британская библиотека.)
Второй вопрос связан с именем Андре Рейснера, немца из Нойштатта, который прибыл к Людовику XIV с непогрешимым, по его мнению, решением проблемы долготы при помощи «одометра» ( Счетчик пройденного пути - Прим. перев) - разновидности корабельного лага, который, как считал изобретатель, может измерять не только скорость корабля при погружении инструмента в воду, но и скорость на суше. «Он обратился к королю и получил письмо, из которого фактически следовало, что Его Величество берет на себя финансирование открытия, благодаря которому все народы получат пользу, и обещает выплатить изобретателю единовременно 60 тыс. ливров, а также гарантирует ему право получать 4 су за каждую тонну грузоподъемности от всех судов, воспользующихся его открытием. Его Величество обязуется выплачивать награду до тех пор, пока общая сумма не превысит 8 тыс. ливров в год, сохраняя при этом за собой только возможность отменить это право по выплате 100 тыс. ливров. Единственным требованием, предъявляемым к изобретателю, была необходимость продемонстрировать эффективность своего изобретения перед господами Кольбером, Дюкеном, генерал-лейтенантом военно-морского флота Его Величества, и членами Академии наук господами Гюйгенсом, Керкви, Робервалом, Пикаром и Озу». Члены комиссии, назначенной королем, встретились в должное время и пришли к выводу, что хотя это устройство весьма остроумно, оно не позволяет определять долготу с какой-бы то ни было точностью. «От немца потребовали письменно ответить на все вопросы, поставленные академией, и он это сделал; но даже обещанные 160 тыс. ливров не смогли его вдохновить на ответы, которые могли бы опровергнуть выдвинутые против его изобретения возражения» [31]. Таким образом, Рейснер так и не получил обещанных денег. Эта история показывает, насколько большое значение Франция придавала решению проблемы определения долготы в открытом море. Можно сказать: «Решение долготной проблемы должно быть таким же величайшим благом для человечества, как и для автора решения; большие награды обещаны любому, кто бы ни решил первым эту проблему. Действительно, те, кто видел, как много людей билось над решением задачи о квадратуре круга, хотя это не могло им принести ничего, кроме славы, не могли оставаться равнодушными к определению долготы, так как решение этой проблемы могло им дать не только славу, но и несравненно более ощутимую выгоду» [32]. Поиск нужного решения этой проблемы на долгие годы занял умы множества людей.